The Ford Territory Problem

When you Google ‘what changes between having 3 and 4 kids’, one of the most common observations is the need to buy a larger car. Purchasing a ‘people mover’ was something we put off for a while, and a two year COVID production delay on our car of choice (a Kia Carnival) also didn’t help the situation!

This meant for a lot longer than necessary, we tried to squeeze everyone into our 7-seater Ford Territory (on the upside, our teens did become mastery level performers at the 'Fosbury Flop' technique. They needed to perform the 'flop' because having two car seats in the middle row prevented it from reclining, so they needed to 'flop' over to the back row. I was certainly less than ideal😯).

I have noticed that my eyes are constantly drawn to Ford Territory and Kia Carnivals cars. Google tells me this is a cognitive bias called the Baader-Meinhof phenomenon. Basically, your brain focuses on a certain thing and suddenly you see that thing everywhere you look!

One thing I have noticed with Ford Territories, is they seem to have a common issue (which I notice because our Territory has the same 'issue'). The latch on the 'sunglass compartment' which sits on the dashboard wears over time, and eventually this compartment refuses to shut.

This issue is VERY annoying on many levels- including the fact it impedes my vision out the front windscreen (which is a little ironic because the compartment is designed to hold items (sunglasses) that support my vision!)

According to my mechanic, this is a problem he sees over and over in the Territories he works on. He tells me it is quite difficult and expensive default to fix.

I told him not to worry, I would just try some duct tape.😉

The Ford Territory problem made me think of our students. There are ‘common problems’ that pop up over and over in maths classrooms. If we are able to identify these as a teaching team, we can take steps in our planning to ensure we put in place the conditions to navigate these with our students. As you have heard me mention before (and I will no doubt continue to mention!), I strongly believe that with deeper Pedagogical Content Knowledge of how children learn Mathematics and the best ways to teach them, we can design sequences that navigate the common 'pitfalls' and ensure our instruction is clear, concise, unambiguous, efficient and evidence-informed.

No fluff, just high-quality instruction.

I have written before about some of the 'thinking mistakes' I commonly observed in my PhD research into place value. Being aware of the 'common problems' students face is a critical part of quality maths teaching.

In this blog I wanted to share a very short sequence of learning related to halving a collection and how an appreciation of common issues allowed me better support student learning. Basically, when we know more, we can 'do better' in our teaching!

After all, slides do not 'teach', it is teachers with high levels of PCK that teach!

Halving is a critical skill that has close links with doubling. When we double a collection, we have a group of a particular size, we then create another group which is the same size and the 'output' is the resulting new whole. So, if we have 5, we need to create another group of 5, and the resulting collection is 10.

Double 5 is 10.

Halving is the inverse. It involves taking the whole (in this case a collection) and partitioning it into two groups of the same size. For example, if we have a collection of 10 items, to halve it, we would make 2 groups of 5.

Half of 10 is 5.

Last week I was working with a Year 2 student in a Tier 3 setting to develop their understanding of halving numbers between 20 and 100. Along the way there were several Pedagogical Decisions I made to ensure the success of my teaching. I have highlighted some of these decisions with a ✅

My teaching is always informed by data I gather from the students I am teaching ✅. With this student I had previously worked through a sequence looking at 2-digit place value, followed by doubling numbers to 100. Before planning the halving sequence, I checked she was fluent in doubling and halving numbers up to 20. I knew these were what the research sometimes refers to as antecedent (or pre-requisite skills), required for success. I knew exactly where to start my teaching and I was confident she had the necessary schema in place to take on the next piece of instruction.

Next, I carefully chose the materials I was going to use to model halving ✅. I selected Unifix blocks because we had worked with them previously when I introduced 2-digit place value, they easily allowed us to both represent tens, and are simple and easy to snap into two parts. I also used a template I created which allowed us to clearly model two parts (see below). 

We started by looking at the even decade numbers- 40,60,80 and 100. I purposefully chose these numbers as I wanted to reduce the cognitive load for my student ✅. By just focusing on tens (and not having to also navigate ones) and by only using even numbers of tens I was able to efficiently and clearly introduce the idea that we can halve the tens.

I made the number 40 with 4 unifix towers with 10 blocks in each (all 10 the same colour), and asked my student: "How many tens are in this number, and how do we say this number?" Both of these questions were designed to allow the student to retrieve their knowledge around the previous work we had done in place value, and signal to her brain that these were concepts we would need today ✅.

She replied: There are 4 tens and the number is forty. This also acted as a Check For Understanding✅ (CFU) which provided me with data to confirm I could continue with my planned sequence as the place value knowledge I knew would be required was in place🙌!

In planning the lesson, I had thought carefully about the language I wanted to use as I modelled the act of halving. I wanted it to be clear, concise and accurate✅. As I moved the materials I stated, "I am going to halve 4 tens. Halving is taking a whole and partitioning it into two parts that are the same. I have 4 tens. I can place 2 tens here (placing them on the red part of the template) and 2 tens here (placing them on the blue part of the template). I am checking there are the same number in the red and blue parts of the template, and there are, so I know that half of 4 tens is 2 tens or I can say that half of 40 is 20."

I modelled and narrated this process for the student ✅. By using phrases such as 'I am checking there are...' I was showing the student my thought process. This is very important in the 'I do' phase of teaching. As the expert I wanted to show the student what was going through my mind as I was completing the halving. Sometimes as experts we forget to narrate our thinking and decision-making processes, because the expertise curse means we forget that we even do this, but novices need to see and hear this to make it part of their schema.

Next, working alongside each other ('We do')✅, we worked through the same process for halving 60, 20 then 80 and finally 100. Each time the materials, language and process remained exactly the same, and with each new number, I was able to step back the level of scaffolding and prompts I provided because she became more and more confident and independent. I purposefully watched, listened and made the necessary adjustments to make sure my inputs aligned with the level of support she required ✅. 

Next, using my teacher judgement✅ I decided she was ready to look at numbers with an odd number of tens (30, 50, 70, 90). My PCK told me that this would be a step up in difficulty, so I circled back to the 'I do' phase ✅. 

This time I modelled using 3 tens. I placed 1 ten in each of the red and blue parts of the template, but there was one ten remaining. I said 'I need to halve this 1 ten, so I am going to break it into 10 ones and that will help me' I then partitioned the 10 ones individually. I then checked each part of the template had the same amount of blocks and stated: 'Half of 30 is 15'.

Together we followed the same process for 50. 'We do'✅

Again, we used the unifix, and again there was the pesky problem that there was 1 ten that we needed to rename as 10 ones and partition individually. Together we modelled this.

You can see how we modelled half of 50 below.

Next, we looked at the same number (50), but this time I suggested we use two different coloured unifix for the 'extra' ten, so we could more efficiently partition it into 5 (light blue) and 5 (dark blue).

This helped to lessen the cognitive load of having to halve the collection of 10 ones by ones, and helped her to generalise that each time we halved 1 ten, it would be 5. We then applied this technique to work out half of 70.

You can see this below:

Finally, we looked at halving 90. By this point the student, had been provided with such a clear sequence of learning that this was no problem for her.

By now, my teaching sequence was complete and through my interactions and observations ✅of the student I was confident that she understood the concept and could execute the process of halving. I decided it was time for her to make some further steps towards consolidating these ideas in her long-term memory through Independent Practice ✅.

I provided her with a list of halves to work through independently (20, 30, 40, 50 ,60,70, 80 ,90, 100). By providing these in order I wanted to see if the student would notice any patterns as she worked through the halving examples. She did!

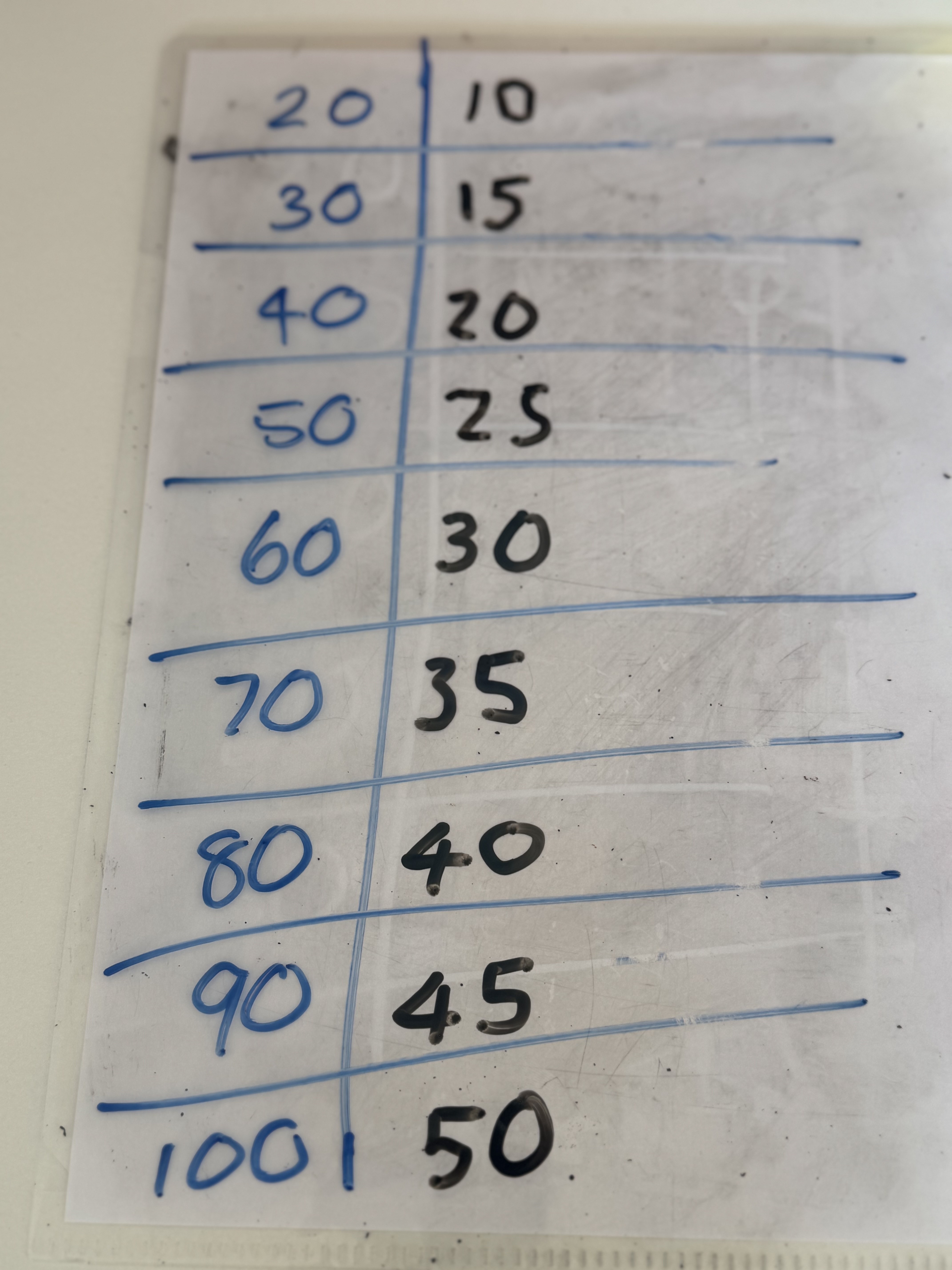
She said: 'Oh, I get it, there is a pattern here in the ones:5,0,5,0!'

This was what I was hoping for!

I then said: which numbers have a '5' when you calculate their half?

She said: Every second one!

I wanted to push her to be more precise in her language and understanding.✅

I said: What do you notice about the number of tens in every second one?

She said: Oh! They are an odd number of tens!

This was a great point to get to in the teaching. I was very happy with our progress, and I could tell the student was feeling a huge sense of success. There is nothing better than when a lesson is a success!

In my mind, I had already started to plan what we would work on next session:

• Calculating halves with numbers which have an even numbers of tens and ones (46,28,86)

and

• Calculating halves with numbers which have an odd number of tens and even number of ones (Eg: 36,78)

Then I would take this learning, and link it to halving in the context of number lines.

Purposeful, responsive, high impact, data-informed teaching ✅

This week I encourage you to think of a common issue your students are struggling with in maths- it might be doubling, halving, number lines, renaming, bridging, adding fractions or linking fractions to decimals to percentages. Take some time to think about how you could create a sequence that would break the teaching down into small and manageable chunks. Think about the pedagogical approaches and techniques that might be appropriate. Think about the pre-requisite skills required, the models you could use to support your teaching, the assessment that you could use, the examples you might and might not use, the retrieval practice you could include in your teaching, the CFU that might be appropriate, the questions you will ask, the language you will use. Do some metacognition (thinking about your thinking), some self-reflection on your teaching, and if possible have a discussion with your teaching colleagues about the sequence to further build your collective capacity!

I promise you, the more deeply you think about your instruction, the better it will become! 

Have a great week!

Ange🎓🎲

P.S. Apologies if all of a sudden you start seeing Ford Territories with their sunglass compartment sticking up as you drive... you can blame me (and the Baader-Meinhof phenomenon taking place in your brain).